Approximator
Во имя Аллаха, Всемилостивейшего и Милосердного
Ю. В. Решетов
Скачать свежую версию
Аппроксиматора в виде файла approximator.jar можно ЗДЕСЬ
Запуск программы после
инсталляции Java из командной строки:
java -jar approximator.jar
Собственно говоря, я вовсе не собирался
опровергать какие либо теоремы, а всего
лишь решал задачу формализации. В
результате чего удалось создать алгоритм, с
помощью которого любое логическое
выражение можно записать в арифметической
форме. До сего момента с помощью логических
выражений можно было оперировать
арифметическими формализмами. Примером
тому являются компьютеры, где все операции,
включая арифметические выполняются с
помощью логических элементов. Обратной
возможности не существовало, точнее были
попытки, но не было строгих обоснований.
Например, Л. Заде разработал нечеткую
логику (fussy logic), которая стала причиной для
упреков со стороны математиков.
Полученные мною результаты опровергают
Вторую теорему Геделя о якобы неполноте
формальных арифметик, на том основании, что
Геделю удалось обнаружить неоднозначности в
формальной системе на базе Теории чисел
Пеано. Вся работа Геделя пошла коту под
хвост, поскольку действительно можно
соорудить такую формальную систему,
которая будет содержать в себе явные
противоречия. Но это вовсе не значит, что
все формальные системы противоречивы.
Просто, Б. Рассел и А. Уайтхед с помощью
своих домыслов и неверных измышлений
изложенных в "Основаниях математики",
а также Г. Фреге и Г. Пеано завели науку в
тупик, наподобие И. Сусанина, полагая, что их
"теории" абсолютно верны. На самом деле
вся их деятельность сводилась лишь к
рассмотрению частных случаев, в которых К.
Гедель обнаружил явные противоречия.
Поэтому нет дальнейшего смысла
рассматривать измышления этих авторов, а
встретив фамилии: Б. Рассел и А. Уайтхед, Г.
Фреге или Г. Пеано, следует сразу же знать,
что все содержимое, сочиненное данными
авторами - бездоказательная ахинея.
Вторая проблема
Гильберта решена
положительно.
В 1895 г. знаменитый генератор
гипотез Д. Гильберт предложил программу
построения всей математики на базе
конечного числа аксиом. Т.е. имея некий
набор аксиом, можно было бы с помощью
дальнейших правил вывода построить все
теоремы. До сего момента предполагалось,
что К. Гедель с помощью своей второй теоремы
якобы доказал невозможность решения данной
проблемы. Но на самом деле, как выяснилось,
он лишь доказал противоречивость некоторых
генераторов ахиней, причисляющих себя к
числу "математиков". Вторая проблема
Гильберта разрешена положительно, т.к. для
ее реализации необходимо и достаточно
всего лишь двух аксиом, тождественно
связывающих логические и арифметические
выражения:
| Логическое выражение |
Арифметический аналог |
| A и В |
А * В |
| не А |
1 - А |
Все остальное можно вывести из
этих двух. Арифметика и логика оказываются
связанными и взаимотождественными, не
говоря уже об отсутствии каких бы то ни было
противоречий.
Решение проблемы
аппроксимации
В основе алгоритма лежат аппроксимации -
переводы числовых последовательностей в формулы. По сей момент
существовало множество различных алгоритмов аппроксимаций, но точным
был только алгоритм перевода последовательности бит в логические
выражения (нормальные конъюнктивные и дизъюнктивные формы). Поскольку,
удалось провести парралель между логикой и арифметикой, а также создать
алгоритм, способный формализовать любую конечную последовательность бит
в арифметическое выражение, то проблема аппроксимации считается
решенной. Остальные алгоритмы попросту теряют свой смысл по причине
низкой точности.
Решение проблемы
автоматического
доказательства теорем
Эта проблема была наиболее важной в
течении XIX - XX веков. К ее решению пытались подступиться через
формальные системы путем символьной обработки информации (распознавание
образов). Собственно она и была самой главной проблемой, вокруг которой
крутились все остальные. Вторая проблема Гильберта также имеет решение
посредством разрешимости доказательства теорем. Суть сводилась к тому,
что если взять два неких формальных выражения, то необходимо было
доказать является ли одно из них выводимым из другого - разрешимым.
Например, если одно выражение является аксиомой, то второе в случае
разрешимости уже теоремой. Если прежние методы предполагали обработку
символьной информации через правила вывода, как это делают обычные
математики, то в результате конечной цели можно было и не достичь
вовсе, например, если правила не имели противоречий, но приводили к
зацикливанию. Либо цель сложно было достичь, если для приведения
одного выражения в другое необходимо было применить огромное количество
правил. Возникала цепная реакция, поскольку путь к решению нередко был
одним единственным, а каждый шаг на этом пути распадался на перебор
вариантов всех правил. Из-за чего для двух любых формальных выражений
невозможно было выяснить, являются ли они разрешимыми относительно друг
друга, если для выяснения этого вопроса, необходимо было применить
более одного правила. На сей момент этой проблемы не существует.
Поскольку любое логическое или арифметическое выражение можно
однозначно записать в виде последовательности бит (число), а
также, из любого числа получить однозначно соответствующее ему
выражение, то значит, для выяснения разрешимости двух выражений
достаточно лишь сравнить оба числа. Точное совпадение всех ненулевых
бит и есть полная разрешимость. Необходимость в промежуточных
символьных преобразованиях отпала сама собой.
Следует уточнить, что в математике разрешимыми являются задачи,
доказано имеющие хотя бы одно решение, независимо от вычислительных
затрат на поиск решение. Предполагается, что для поиска можно
использовать мифическую машину А. Тьюринга, "способную"
выполнять любое количество параллельных
операций за один
такт. Поэтому вопрос о разрешимости - вопрос о том, стоит ли вообще
запускать машину Тьюринга.
Использование алгоритма
Алгоритм заложен в программную реализацию,
с помощью которой можно перевести любой цифровой поток в формальное
арифметическое выражение. По умолчанию считается, что данным потоком
являются последовательность байт. Например, чтобы узнать, как
арифметически формализуется логическое выражение A или В, составим
таблицу истинности:
Переменные
|
Результат
|
N1
|
N2
|
N1
или N2
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
Результирующая последовательность 0111 и
будет основой для формализации логического выражения. Запишем ее
в текстовый файл.
0
1
1
1
сохраним файл на диске под именем or.dat
(можно любое другое). Запустим программу и откроем в ней этот самый
текстовый файл. Получим формулу:
n1 - n1 * n2 + n2
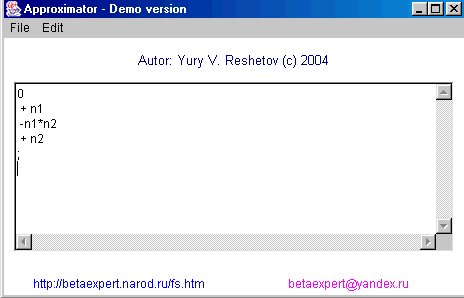
Проверим полученную формулу,
подставив вместо n1 и n2 значения взятые из таблицы. И убедимся, что
она выдает 0
только когда и n1 и n2 одновременно имеют нулевые значения, а 1 во всех
остальных трех случаях. Попробуем проделать тоже самое с исключающим
ИЛИ.
Переменные
|
Результат
|
N1
|
N2
|
N1
либо N2
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
0
|
Получим формулу:
n1 - 2 * n1 * n2 + n2
Как и положено, эта формула дает на
выходе 0 если оба значения переменных равны между собой и 1, если они
различны.
Для аппроксимации других числовых последовательностей можно указывать
значения отличные от 0 и 1. Можно формализовывать и бинарные файлы,
если открыть их в меню, как таковые.
Закон о неразрешимости интерполяций и экстраполяций
или Закон абсолютной непредсказуемости
он же Закон о бесполезности индуктивного метода (не путать с
дедуктивным),
а также Антикорреляционный Закон
Точность аппроксимации и однозначность
соответствия логических и арифметических выражений соответствующим
числам не позволяет произвести манипуляции, которые совершил Курт
Гедель по отношению к формальной системе Пеано в области определения
формализмов. Там он присвоил всем
символам произвольные номера, "взятые с потолка" и перетасовывая их,
поставил систему "в тупик", "обнаружив" доказательство того, что ФС
одновременно "врет" и одновременно же говорит "правду", т.е. содержит
выражения одновременно и ложные и якобы по признанию самой системы,
истинные. Суть шулерства Геделя сводится к тому, что он получил
равенство:
одна последовательность чисел =
другая последовательность чисел
Именно наличие подобных
неоднозначностей, заложенных Г. Пеано в якобы "теорию чисел" и
позволили прийти к подобному результату.
В алгоритме данного аппроксиматора такие "фокусы" не пройдут, поскольку
соответствием между двумя выражениями является лишь абсолютное
равенство двух последовательностей чисел с точностью до бита из которых
они образованы.
одна последовательность чисел = точно
такая
же последовательность чисел
А сами последовательности также не могут быть произвольными, а как
видно из примеров, являются результатами точных аппроксимаций (для
логических выражений - аппроксимация битов таблиц истинности).
Предположим, что в результате эксперимента мы получили некую
зависимость в виде ряда значений y(x):
X
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
Y
|
0
|
1
|
4
|
9
|
16
|
25
|
?
|
0 1 4 9 16 25 ... ?
Каким должно быть значение функции y(x), если значение x = 6 ?
Элементарный вопрос экстраполяции. Если прогнать метод наименьших
квадратов, покажет, что значение функции должно быть равным 36. А
теперь
попробуем доказать, что если ряд начинается со значений 0 1 4 9 16 25,
то его продолжение в виде значения 36 вовсе не является однозначно
доказуемым. Доказательство проведем от
обратного, т.е. докажем, что первые шесть значений нашего ряда никоим
образом не являются причиной для того, чтобы выяснить точное значение
последующих чисел ряда. Предположим, что седьмым числом нашего ряда
должно быть число -7. Запишем нашу гипотезу и создадим текстовый файл
следующего содержания:
0
1
4
9
16
25
-7
Запустим аппроксиматор и получим формулу:
у = n1 + 4*n1*n2 -7*n1*n2*n3 + 8*n1*n3
+ 4*n2 -27*n2*n3 + 16*n3
Так какая же закономерность верна? y =
x^2 или у = n1 + 4*n1*n2 -7*n1*n2*n3 + 8*n1*n3 + 4*n2 -27*n2*n3 +
16*n3, где x - есть функция от n1, n2 и n3 по бинарному разложению.
Ведь в обоих случаях первые шесть значений ряда абсолютно одни и те же.
Ответ прост! Если значение при каком либо аргументе прямо не
формализовано в определении функции - выходит за пределы области
определения функции, то оно является неопределенным и недоказуемым
(неразрешимым). В таком случае
получается, что если в результате эксперимента были получены какие либо
данные, то за пределами этих экспериментальных данных - экстраполяция,
а также в промежуточных значениях - интерполяция может быть заведомая
ошибка. А
следовательно любые неэкспериментальные выводы, но сделанные по
результатам
эксперимента, можно считать недоказуемыми. Логически, так оно и есть.
Тому можно привести множество примеров. Например, множество функций,
которые при одних областях значений аргументов дают хорошие приближения
к каким либо простейшим функциям, зато при остальных значениях
аргументов абсолютно с теми же красивыми значениями функций абсолютно
не совпадают. Теория вероятности говорит весьма прямолинейно, что
вероятность изменения ситуации абсолютно независима от закономерностей
обнаруженных по результатам наблюдений прежних ситуаций.
Также и Гедель опростоволосился со своей псевдотеоремой: обнаружив
наличие неполноты только лишь в формальной системе Пеано, огульно
распространил вывод на все остальные арифметики без исключения. Кто ему
виноват,
что он таким идиотом оказался?
Именно присутствие точности и однозначности является и причиной того,
что формализм заложенный в алгоритм аппроксиматора делает абсолютно
бессмысленным всякие интерполяции и экстраполяции (за исключением
экстраполяций периодических функций). Любые данные можно коррелировать
с любыми другими данными. Например, данные полученные экспериментально,
подогнать под корреляцию с данными взятыми с потолка или высосанными из
пальца.
Поскольку интерполяции и экстраполяции имеют явную неоднозначность,
неразрешимость, неполноту и противоречивость, то отсюда следует
вывод
о том, что значения функций полученные по результататам
применения
любой
интерполяции или экстраполяции являются недоказуемыми и
могут
рассматриваться лишь в контексте гипотетического приближения.
Применение метода математической индукции с сего момента перестает быть
доказательством чего бы то ни было. А статистика лишается излюбленных
корреляций.
Из этого вовсе не значит, что надо немедля запретить пользоваться
интерполированием и экстраполированием функций, а всех, кто ослушается
бить нещадно батогами. А отсюда следует вывод, что теоретически и
по
результатам экспериментально полученных данных, можно вывести
закономерность "подтверждающую" любые, в т.ч. и самые бредовые теории -
подогнать желаемое под действительное.
Конечно же все вышесказанное уже отметает метод математической
индукции, выходящей за пределы определения функций, но зато утверждает
абсолютную непогрешимость дедукции, отсекающей заведомо нелогичные
варианты.
Вообще то, меня удивляет, что юристы к такому повороту дел подготовлены
гораздо лучше математиков. Дедуктивный метод используется ими не первый
день. А презумпция невиновности не позволяет огульно обвинять кого бы
то ни было в чем бы то ни было, несмотря на то, что прежняя биография
подозреваемого чудесно коррелируется с расследуемым преступлением.
Никакой индукции и прочих вольностей, столь излюбленных математиками,
юристы не принимают в качестве доказательства. Только дедукция, путем
пересечения множества подозреваемых с множеством улик до тех пор, пока
в оставшемся подмножестве не останется тот, кого следует уже привлечь к
ответственности.
Теорема о границах полноты, разрешимости и
непротиворечивости формальных
арифметик
Коли "теорема" Курта Геделя является
всего лишь частным случаем, то соответственно уже не является теоремой,
а всего лишь доказательством неразрешимости некоторых формальных
арифметик. Остается выяснить последний вопрос: какова же должна быть
формулировка полной теоремы?
В 1921 г. Э. Пост доказал теорему:
"Формула является доказуемой в
исчислении высказываний, если она является тождественно истинной во
всех интерпретациях исчислений высказываний"
Этот результат Э. Пост получил с помощью строго обоснованного в
1932 г. им же метода таблиц истинности. Он почти подошел к решению
полученному мною. Но не смог обосновать вывод о том, что
исчисление высказываний является разрешимой формальной системой. В
результате чего на тот момент, трудность состояла в том, что для
подобного обоснования, предполагалось построить систему с
использованием рекуррентных рассуждений и переходами на более высокие
уровни. Причиной тому было незнание возможности существования полной и
обратимой аналогии между арифметическими и логическими выражениями,
которые я реализовал в своем алгоритме. А посему в формальных системах
не считалось обязательным соблюдение соответствий между теоремами и
таблицами истинности, чем и воспользовался Курт Гедель.
Поскольку я прошел этот этап успешно, то вместо псевдотеоремы Геделя,
использовать теорему Решетова:
"Формальная
арифметика является полной, разрешимой и непротиворечивой в том случае,
если и только если, ее формализм является строго аппроксимирующим"
А это
означает, что непротиворечивая формальная система даже не ограничена
только тождественно истинностными интерпретациями исчисления
высказываний, как предполагал Э. Пост, но и имеет более широкий
диапазон, охватывая также и тождественно истинностные
арифметические интерпретации.
Вполне понятно, что во времена Геделя и Поста подобную теорему вывести
было невозможно, т.к. алгоритм строгой арифметической аппроксимации был
еще неизвестен, а существующие алгоритмы, являлись лишь сглаживающе -
уточняющими (давали приближенные результаты). Поэтому, вместо строгой
теоремы о существовании непротиворечивой арифметике можно было лишь
предполагать гипотезы. Слава Аллаху! С этим безобразием покончено раз и
навсегда!
Прикладное применение аппроксиматора
Осталось лишь выяснить последний вопрос
о возможности полезного применения аппроксиматора. Это самый трудный
вопрос. Когда Майкла Фарадея спросили о практическом применении
электричества, законы которого он сформулировал, то незадачливый ученый
ответил, что насчет практической пользы у него большие сомнения, а вот
в том, что его открытие будет обложено налогом, он нисколько не
сомневается. Тут все понятно, ведь появление налоговой инспекции -
самая предсказуемая закономерность.
Также и у меня сомнений о пользе аппроксиматора больше чем
предостаточно. По моему, ничего окромя вреда это не даст. Пока я искал
материалы по второй псевдотеореме Геделя в Интернет, то каждая такая
вылазка, сопровождалась добычей столь бредовых идей, о которых даже сам
Гедель не догадывался, ведь на основе его ахинейной "теоремы", другие и
не менее ахинейные теоретики умудрились доказать бесполезность всего и
вся. Явно, пользы никакой не будет, также, как и от
24
проблемы Гильберта.
Очевидно, что наибольшую пользу извлекут только околонаучные мошенники,
которые всюду пытаются торговать бредовыми теориями. Просто раньше это
было для них сложнее, а теперь сплошная малина. Ведь любой желающий
может теперь заняться сочинением любых закономерностей. Например, можно
взять данные, собранные метереологами о среднегодовой температуре за
все известные прошлые периоды, дописать к ним отсебятину из любых цифр,
например, весьма отрицательных. Потом, результаты прогнать через мой
аппроксиматор и получить формулу согласно которой в 2008 г. должен
наступить новый Ледниковый период. Если обыватель не знаком с моим
Законом о неразрешимости интерполяций и экстраполяций,
то он будет жестоко обманут, согласно Платону, благодаря которому
незнание Законов не освобождает от лохотронов. Ведь несчастные ротозеи
даже если попытаются проверить всученную им таким макаром формулу и
подставят в нее какой либо год из периода предыдущего, то лишь убедятся
в том, что все данные совпадают очень точно. В результате чего,
мошенники могут нажиться на доверии олухов, например, начав активную
распродажу теплых вещей и топлива. Каково же будет удивление
простодушных, когда они встретят 40 градусную жару, облачившись в
меховые шубы, шапки и унты и сидя на разогретой добела печи.
Другим примером моего научного вредительства может стать использование
того же самого
Закона с целью делания выводов о том,
что якобы вообще никакие закономерности не имеют никакого смысла. Опять
же, если ротозей не будет знать что интерполяции и экстраполяции
выходят за пределы определения функции, то его легко будет обмануть,
например, "утверждая", что дедуктивный метод более "недействителен". Но
ведь дедукция, в отличие от индукции, как раз содержит данные лежащие в
пределах определения и лишь отсекает заведомо неверные выводы.
Впрочем сам Давид Гильберт неоднократно предупреждал, что решение
затронутых им проблем, может привести к проблемам не меньшим. Курт
Гедель надул и Гильберта и Поста, но не слишком надолго. Все тайное,
рано или поздно становится явным.
Приложение.
23 из 24 проблемы Давида Гильберта из доклада, прочитанного им 8
августа 1900
г. на II Международном Конгрессе математиков в Париже:
-
Проблема Кантора о мощности
континуума
-
Непротиворечивость
арифметических аксиом
-
Равенство двух тетраэдров с
равновеликими
основаниями и равными высотами.
-
Проблема о прямой как кратчайшем
соединении двух точек.
-
Понятие непрерывной группы
преобразований
Ли, без предположения о дифференцируемости функций, определяющих
группу.
-
Математическое изложение аксиом физики.
-
Иррациональность и трансцендентность
некоторых чисел.
-
Проблема простых чисел.
-
Доказательство наиболее общего закона
взаимности в любом числовом поле.
-
Задача о разрешимости Диофантова
уравнения.
-
Квадратичные формы с произвольными
алгебраическими числовыми коэффициентами.
-
Распространение теоремы Кронекера об
Абелевых полях на произвольную алгебраическую область рациональности.
-
Невозможность решения общего уравнения
седьмой степени с помощью функции, зависящей только от двух переменных.
-
Доказательство конечности некоторой
полной системы функций.
-
Строгое обоснование исчислительной
геометрии Шуберта.
-
Проблема топологии алгебраических кривых
и поверхностей.
-
Представление определенных форм в виде
суммы квадратов.
-
Построение пространства из конгруэнтных
многогранников.
-
Являются ли решения регулярной
вариационной задачи необходимо аналитическими?
-
Общая задача о граничных условиях.
-
Доказательство существования линейных
дифференциальных уравнений с заданной группой монодромии.
-
Униформизация аналитических зависимостей
с помощью автоморфных функций.
-
Развитие методов вариационного
исчисления
24. Поймать муху
на обратной
стороне Луны!
Двадцать четвертая проблема Д. Гильберта была изложена вне рамок
вышеуказанного доклада в кругу учеников в 1920 г. с пояснениями:
"Сама эта задача никому не нужна. Но подумайте: если она будет решена,
то, какие могучие методы придется изобрести для этого, и какое
множество других важных открытий мы при этом сделаем!"
|

Давид Гильберт
1862 - 1943
|



